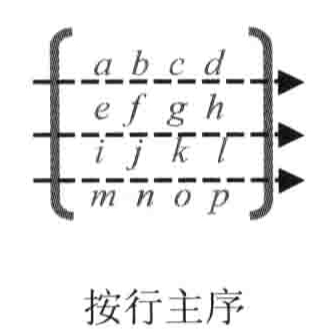
行主序
在内存中排序是按照这种排布的
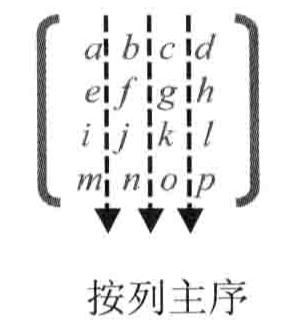
列主序
在内存中排序是按照这样排布的
容易造成误解的点
行主序和列主序,最终呈现的行列式不一样,其实并不是这样的,只是说同一个矩阵在内存中不同的存储方式而已
向量类型、矩阵主序与乘法顺序详解
一、向量类型简介
-
列向量(Column Vector):
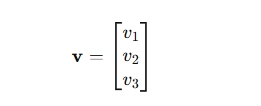
是一个n × 1的矩阵 -
行向量(Row Vector):
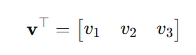
是一个1 × n的矩阵
二、矩阵与向量的乘法规则
-
列向量方式(线性代数标准):
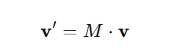
向量在右边,矩阵左乘。
-
行向量方式(某些图形引擎):
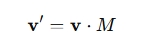
向量在左边,矩阵右乘。
三、行主序与列主序的内存排列
行主序(Row-Major, 如 C/C++):
按行优先的顺序排列:
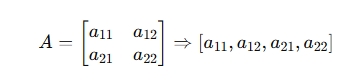
列主序(Column-Major, 如 Fortran / OpenGL):
按列优先的顺序排列:
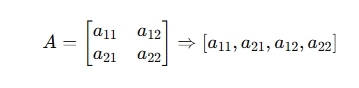
四、列主序 vs 行主序的计算演示
仿射变换矩阵
定义一个二维仿射变换矩阵(3×3):
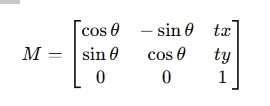
使用一个二维仿射矩阵 --》(旋转 90°),平移 (2, 3) :
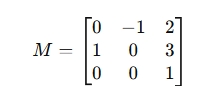
原始点:
- 坐标为(x, y) = (4, 5)
- 齐次列向量:
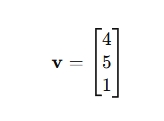
- 齐次行向量:
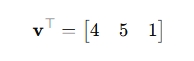
方法 1:列主序 + 列向量(数学 / OpenGL 风格)
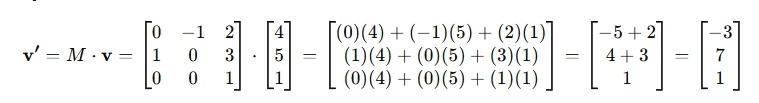
结果:
(x', y') = (-3, 7)
方法 2:行主序 + 行向量(DirectX 风格)
需要将矩阵转置再使用:

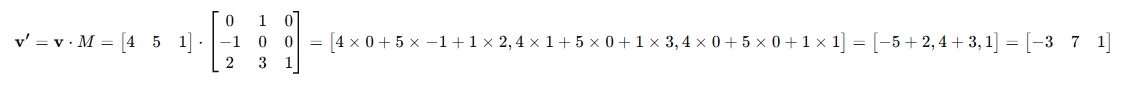
结果:
(x', y') = (-3, 7)
五、总结对照表
| 表达方式 | 向量形式 | 乘法方向 | 内存顺序 | 是否需要转置 |
|---|---|---|---|---|
| 数学、OpenGL | 列向量 | ( M \cdot v ) | 列主序 | 否 |
| DirectX、HLSL | 行向量 | ( v \cdot M ) | 行主序 | 否 |
| 行向量 + 列主序 | 行向量 | ( v \cdot M ) | 列主序 | ✅ 是,需转置 |
| 列向量 + 行主序 | 列向量 | ( M \cdot v ) | 行主序 | ✅ 是,需转置 |
